Regression - Elastic Net, L1(Lasso), L2(Ridge)

suzzal 2022. 1. 19. 23:01

0. Intro

들어가기 전에 머신러닝의 목적을 알아보자면 목적함수를 최적화하는 것이다.

대표적인 목적함수는 오차제곱합(=에러)이고 에러를 줄이는 게 목표이다.

결론적으로 목적함수를 최소화하여 모수추정하는 것이 머신러닝의 목적이다.

1. Regulization(정규화,규제, 일반화)이해

엘라스틱넷, 라쏘, 릿지 회귀를 공부하기 전에 정규화를 먼저 이해해야 한다.

1번 그림은 데이터의 추세와 직선의 기울기의 차이가 나는 것을 볼 수 있다.

2번 그림은 데이터의 추세대로 직선의 기울기가 어느 정도 따라간다.(정규화)

3번 그림은 데이터의 추세대로 직선의 기울기가 완전히 따라간다.(과대적합)

1번의 경우 그림에서 보이는 것과 같이 정확한 예측은 아니다.

2번의 경우 가장 정규화가 잘 된 모델이라 할 수 있다.

3번의 경우 기울기가 데이터에 맞춘 것을 볼 수 있고 이런 경우 데이터가 추가로 입력되었을 때 해당 모델이 정확한 예측을 할 수 없다.

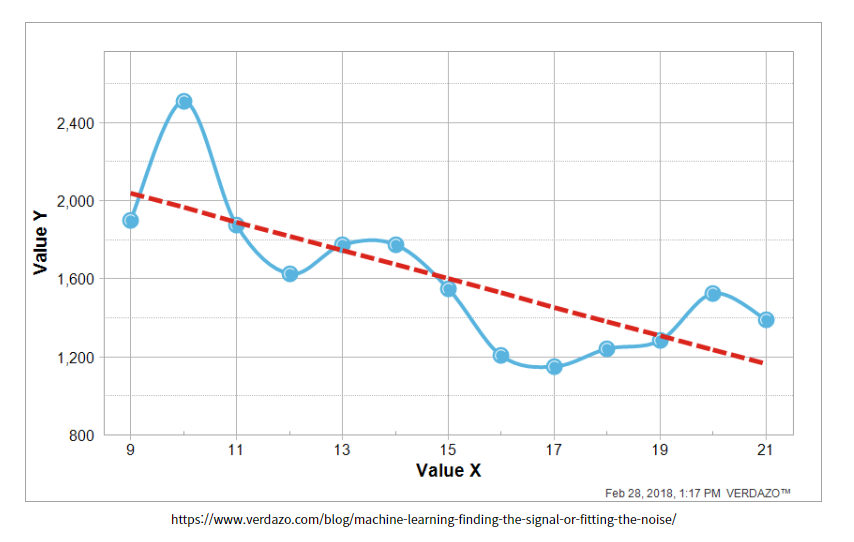
위에서 이해한 내용을 바탕으로 위 그림의 하늘색 선은 overfitting 되었다고 볼 수 있습니다.

따라서 빨간색 선으로 모델이 설정될 수 있게 해주는 작업이 필요한데 해당 작업을 할 때 이용하는 것이 Lasso, Ridge다.

2. Lasso & Ridge Regression

(a)Lasso(least absolute shrinkage and selection operator) Regression

- 정규화 선형회귀로 선형회귀 계수에 대한 제약 조건을 추가하여 모델이 overfitting 되는 것을 막아줌

- feature를 감소시켜 구불구불한 직선을 펴주며 정규화

- 결국 중요한 feature만 쓰겠다는 것

- R에서 glmnet 패키지의 glmnet() 함수

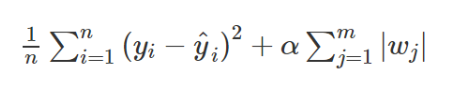
최적화된 모수 = 목적함수 + 패널티(w는 가중치 의미)

α 값을 높이면 (α=1)몇몇 가중치들은 0으로 수렴하고 이에 따라 feature의 수도 감소.

가중치가 0인 중요하지 않은 특성들을 제외해 줌으로써 모델에서 중요한 특성이 무엇인지 알 수 있게 된다.

반대로 α 값을 줄이면(α=0.0001) 상대적으로 많은 feature를 이용하게 되므로 과적합 우려.

(b)Ridge

- 모델의 복잡도 조정

- 가중치를 0의 방향으로 잡아당기는 역할을 한다.(즉, 가중치의 절댓값을 가능한 작게 만들려는 작업)

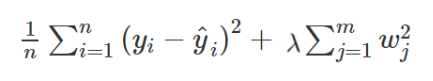
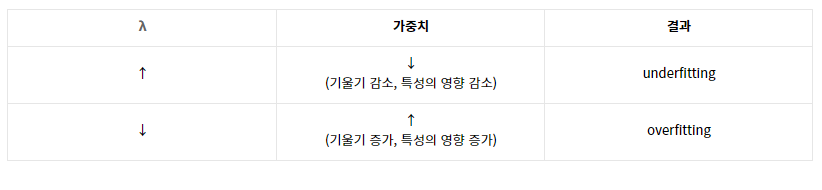
(λ = 0 일 때는 패널티 항은 효과가 없고, 따라서 리지 회귀(ridge regression)은 최소제곱추정치를 생성)

즉, λ(람다)가 패널티를 얼마나 부과하는가를 조절하는 조절 버튼이라고 생각하면 된다.

(c) Lasso & Ridge 비교

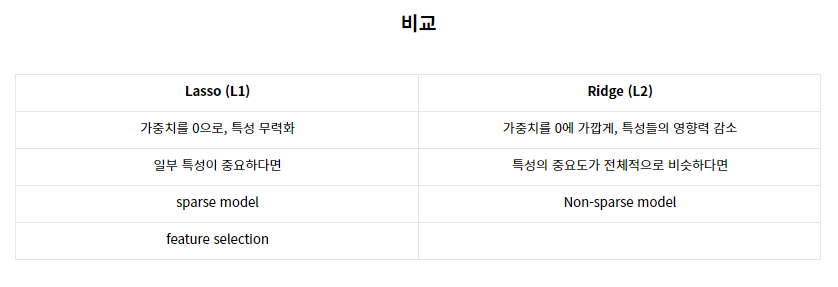
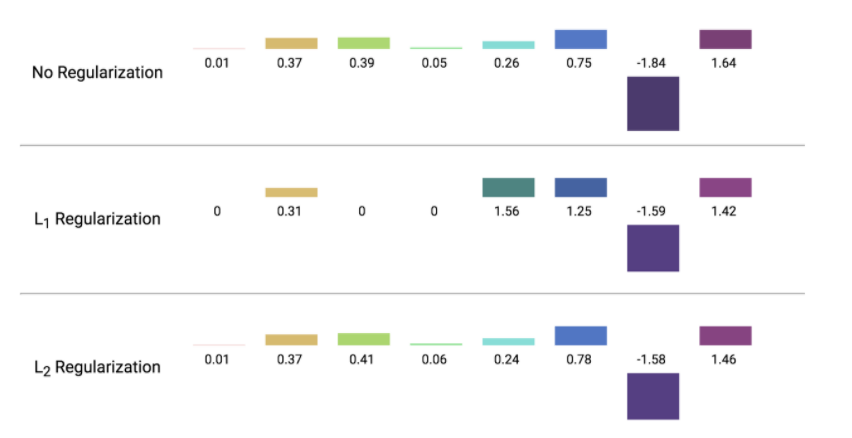
3. Elastic Net Regression

엘라스틱넷 회귀분석(Elastic Net Regression)은 선형회귀의 일종으로

앞서 설명한 정규화 선형회귀인 릿지회귀(Ridge Regression)과 라쏘회귀a(Lasso Regression)를 적절히 절충하여 만든 모델이다.

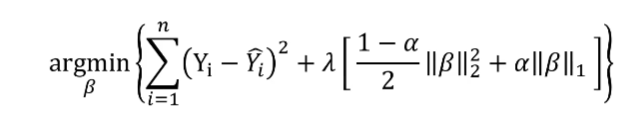
위의 식에서 α값을 0~1 사이 값에서 조절하여 L1,L2 penalty 조절

Reference